ĪĪĪĪ·├┐Ą└Ņ}Ą─┤Ņ}Ģr(sh©¬)ķg▓╗æ¬(y©®ng)│¼▀^15ĘųńŖĪŻ┤░Ė├„╚š╣½▓╝ŻĪ
ĪĪĪĪļyČ╚Ż║Ī’Ī’Ī’Ī’
ĪĪĪĪąĪīW(xu©”)╦──Ļ╝ēŖWöĄ(sh©┤)╠ņ╠ņŠÜŻ║Ėé┘ÉšµŅ}
ĪĪĪĪ(Ą┌╩«ī├╚A▒Ł┘É│§┘ÉįćŅ})╝ūĪóęęā╔╚╦▀M(j©¼n)ąąŲ╣┼ęŪ“▒╚┘ÉŻ¼ęÄ(gu©®)Č©šlŽ╚ä┘╚²ł÷šlä┘,Ą┌ę╗ł÷╝ū.å¢ĄĮ?j©®ng)Q │÷ūŅ║¾ä┘žō(f©┤)×ķų╣Ż¼╣▓ėąÄūĘN▓╗═¼Ą─Ūķą╬?Ųõųą╝ūä┘Ą─Ūķą╬ėąÄūĘN?ĪĪ
ĪĪĪĪĪŠĘų╬÷Ī┐:▓╔ė├śõą╬łD┐╔ęį║▄║├Ąž┐╠«ŗ▒╚┘Éå¢Ņ}Ą─š¹éĆ(g©©)ī”▐─▀^│╠.ū„śõą╬łD╚ńŽ┬Ż║
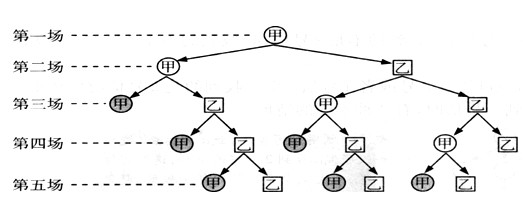
ĪĪĪĪÅ─śõą╬łDųą┐╔ęįŪÕ│■Ąž┐┤ĄĮŻ¼ĄĮ?j©®ng)Q│÷ūŅ║¾ä┘žō(f©┤)Ż¼╣▓ėą10ĘN▓╗═¼Ą─ŪķørŻ¼Ųõųą╝ūä┘Ą─Ūķą╬ėą6ĘN.
ĪĪĪĪļyČ╚Ż║Ī’Ī’Ī’Ī’Ī’
ĪĪ ąĪīW(xu©”)╦──Ļ╝ēŖWöĄ(sh©┤)╠ņ╠ņŠÜŻ║Ėé┘ÉšµŅ}
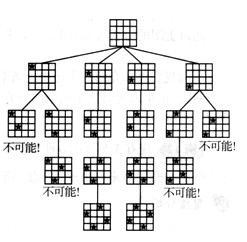
ĪĪĪĪ(Ą┌┴∙ī├"ū▀├└"įćŅ}) 4╗╩║¾å¢Ņ}╩Ūīó4éĆ(g©©)ŲÕūėĘ┼į┌4×4Ą─Ė±ūė└’Ż¼╩╣Ą├▓╗Ģ■ėąā╔éĆ(g©©)ŲÕūėį┌═¼ę╗ąąĪó═¼ę╗┴ą╗“?q©▒)”ĮŪŠĆ╔Ž.(ė├Ž¾ŲÕąg(sh©┤)šZüĒšfŻ¼įōå¢Ņ}╩Ū╚ń║╬īó4éĆ(g©©)╗╩║¾Ę┼į┌4×4Ą─ŲÕ▒P╔ŽŻ¼▓óŪę╩╣Ą├ø]ėą╗╩║¾─▄╣źō¶ī”ĘĮ).
ĪĪĪĪĪŠĘų╬÷Ī┐: ╩ūŽ╚Ż¼Ž┬├µė^▓ņ╚ń║╬ė├śõą╬łDüĒ├Ķ╩÷╗╩║¾Ą─Ę┼ų├.
ĪĪĪĪśõą╬łDųąĄ─├┐éĆ(g©©)Ēö³c(di©Żn)▒Ē╩Š4éĆ(g©©)╗ź▓╗╣źō¶Ą─╗╩║¾Ą─ę╗ĘN Ę┼ų├Ż¼4éĆ(g©©)╗╩║¾Ę┼ų├į┌Å─ū¾ĄĮėę▀B└m(x©┤)Ą─4┴ą╔Ž.
ĪĪĪĪ×ķ▒Ńė┌ś╦(bi©Īo)ūRŲÕ▒P╔ŽĄ─╬╗ų├Ż¼▀@└’░čŲÕ▒P┐┤ū„ę╗éĆ(g©©)4×4Ą─š²ĘĮą╬.
ĪĪĪĪÅ─į┌╬╗ų├(1Ż¼1)Ę┼ų├ę╗éĆ(g©©)╗╩║¾ķ_╩╝Ż¼╚╗║¾Ż¼į┌Ą┌2┴ą╔ŽŻ¼┐╔ąąĄ─╗╩║¾╬╗ų├ų╗ėą(3Ż¼2)║═(4Ż¼2)Ż¼ę“?y©żn)ķ╬╗ų?1Ż¼2)Ģ■ī¦(d©Żo)ų┬ā╔éĆ(g©©)╗╩║¾į┌═¼ę╗ąąŻ¼╬╗ų├(2Ż¼2)Ģ■ī¦(d©Żo)ų┬ā╔éĆ(g©©)╗╩║¾į┌═¼ę╗Ślī”ĮŪŠĆ╔ŽĪŻ▀xō±į┌╬╗ų├(3Ż¼2)Ę┼ų├╗╩║¾Ż¼īó▓╗į╩įS║¾└^Ą─Ę┼ų├;Č°Ę┼ų├į┌╬╗ų├(4Ż¼2)ätį╩įSīó┴Ēę╗éĆ(g©©)╗╩║¾Ę┼ų├į┌╬╗ų├(2Ż¼3).
ĪĪĪĪ╩ŻŽ┬Ą─łD┐╔░┤═¼śėĄ─ĘĮĘ©═Ļ│╔śŗ(g©░u)įņŻ¼ūŅĮK╚ńŽ┬łD╦∙╩Š.
ĪĪĪĪ¼F(xi©żn)į┌Å─śõą╬łDųąŠ═┐╔ęįŪ¾│÷▀@éĆ(g©©)å¢Ņ}Ą─ĮŌŻ¼╝┤ę╗éĆ(g©©)░³║¼4éĆ(g©©)╗ź▓╗╣źō¶Ą─╗╩║¾Ą─Ę┼ų├.