32.馬的舞蹈
至少需要移動16次.最好是想象4個馬作集體移動,它們由角落移向中間的方格,再從中間移向角落,就像在繞著中央的方格作旋轉.這個謎題歷史悠久,在歐洲有文字記載的歷史可追溯至1512年.

33.鐵道支線
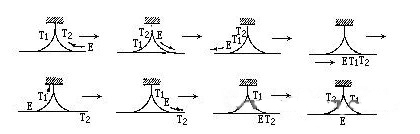
類似的謎題在本世紀初就相當風行.就像其他的類似謎題一樣,這個問題初看并不困難,但實際去做又會覺得很棘手.可以用彩色的積木代表車廂與火車頭以幫助思考.
34.彩色方塊
把每一個邊長1cm的立方體中相連且有一共同頂點的3個面涂上紅色,其他3個相對的面涂上藍色,這樣,這8個立方體就能組合出邊長2cm的紅色立方體,也能組合成邊長2cm的藍色立方體.
組合邊長3cm的立方體要困難得多,最好是能用實物幫助思考.27個邊長1cm的立方體具有27×6個正方形的面,3個邊長3cm的立方體有3×6個面,每個面由9個正方形組成.所以只要正確地著色,就能作出相應的正方形.
在一個邊長3cm的紅色立方體中,有4種不同形式的小立方體.
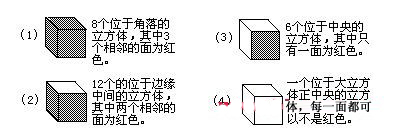
對藍色及紅色的立方體而言,情形也是一樣,因此著色的方法如下:
6個立方體R2B2Y2
3個立方體R3B2Y1
3個立方體R3B1Y2
3個立方體R2B3Y1
3個立方體R1B3Y2
3個立方體R2B1Y3
3個立方體R1B2Y3
1個立方體R3B3 B3Y3 Y3R3(各一個)
R表示紅色,B表示藍色,Y表示黃色,數字則代表著該顏色的面的數目,而且顏色相同的2個或3個面均互相鄰接.
使用符號描述不同的立方體是非常有用的方法.數學家通常也是使用字母與符號描述所面臨的問題,而不是用長篇大論的文字敘述.
35.善妒的丈夫
和上一題一樣,用一些符號來描述問題,對解題會很有幫助.現在用Aa,Bb,Cc表示3對夫妻,大寫字母代表丈夫,小寫字母代表妻子.
在3對夫妻的情況下,船需要來回5次.以下為一種解法:
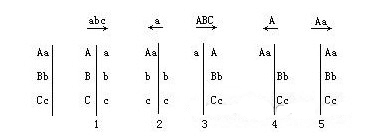
首先3位妻子abc劃到對岸,再由a妻子把船劃回來;然后3位丈夫ABC安全地劃過去,將a妻子留在旅館中;最后,A丈夫回去拯救他勇敢的妻子!
在一些卡片上寫上代表各人的符號,可以幫助你解題.
下列5對夫妻的解法能滿足所有條件,但需要來回13次,也許你可以找到更好的方法.如果讀者發現更好的解法,請告訴本書作者.

首先3位妻子abc先劃到安全地帶,再由a妻子把船劃回去.然后A與他的妻子到對岸,妻子下船,A把船劃回去(由于b和c的丈夫不在場,所以A不能下船).再由ABC劃過去,Aa劃回來,這時Bb與Cc已經到安全地帶.現在由ADE劃到對岸,他們的3位妻子則暫時留在旅館中.A回來接他的妻子,然后再由D與E回來接各人的妻子.
36.延長電線
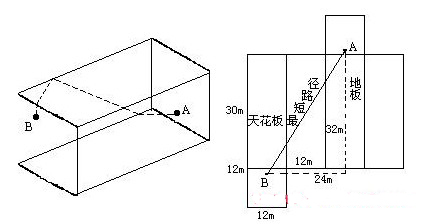
如果你把這個大廳想象成鞋盒,并展開成平面,則由A至B最短的路徑,為橫跨地板、一面墻以及天花板的路徑,長度為40m.
37.聰明的園丁
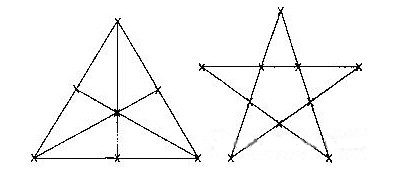
8.周長與面積
你可能會發現,剛開始幾乎都是“碰巧”找到形狀,但不久就覺得有規律可循,使你的方法更具有系統性.
有一種方法是由一個3×3的正方形,或一個4×2的長方形開始,然后想象其邊界可能的變化方式,如圖1所示.
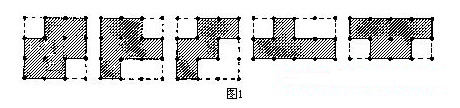
5×1的長方形只有一種解,4×2的長方形則有有限個解.大部分的形狀由3×3的正方形變化而來.從這個活動中可以清楚地看出,周長相同的形狀,面積不一定相同.邊長為3、4與5單位的三角形為直角三角形,由此也可以找出其他周長為12單位的形狀.一些可能的形狀如圖2所示.

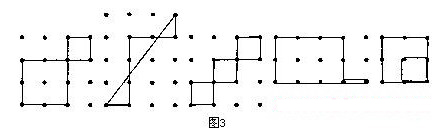
周長為12單位的可能形狀總數,視形狀的種類而定.如果線能夠交叉或重疊,則形狀的數目會變得更多.如果是一組人一起進行這個活動,大家可以討論什么形狀是可以接受的,以及該如何精確地定義“可以在釘板上作出的周長為12單位的形狀”.圖3中的哪些形狀是可以接受的?
39~40.鑲嵌圖案等
在人造的物體中經常可以見到鑲嵌圖案.例如墻上的磚、庭院中的石板路、地毯與壁紙等,都與鑲嵌圖案有關,因為這些都是一再重復基本單元所構成的圖案.
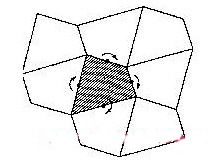
事實上,任何四邊形都可以作為鑲嵌圖案的基本單元.用卡片紙剪下一個四邊形作為樣板.由一個四邊形(陰影部分)開始,輪流繞每一邊的中點,將四邊形旋轉180°.



